Yapay Zekâ ve Makine Öğrenmesinin İstatistiksel Temelleri
İstatistik, yapay zekâ ve makine öğrenmesinin güçlü bir temelidir. Bu yazının birinci bölümünde dört temel istatistiksel makine öğrenmesi algoritması özetlenmiştir. Algoritmalar kısaca açıklanmış, Python ile oluşturulan örnek grafikler ve kodlar sunulmuştur. İkinci bölümde istatistiksel öğrenme ve makine öğrenmesinin detaylı karşılaştırması yapılmıştır.
Yapay zekâ, topladığı devasa veriler arasındaki ilişkileri belirlemek ve onları kümelendirmek için istatistiksel veri analizini yoğun olarak kullanır. Karşılaştığı yeni durumları/sorunları bu devasa veri kümeleri ile ilişkilendirerek uygunluk olasılığı en yüksek cevapları ve çözümleri bu veri kümelerinden seçer. Her soru veya sorun ilişkilendirmesi analiz edilerek öğrenme süreci devam eder. İstatistik, yapay zekâ ve makine öğrenmesinin pek de görünmeyen temelidir aslında.
ve Ön İşleme"] --> B{"İstatistiksel
Analiz"} B --> C["Modelleme
ve Algoritmalar"] C --> D["Makine Öğrenmesi
Süreci"] D --> E["Tahmin,
Karar Verme"] E --> F["Geri Bildirim
ve Güncelleme"] F --> B %% Renk paleti yumuşatıldı style A fill:#FFF4CC,stroke:#E6B800,stroke-width:2px,color:#333 style B fill:#E7FAD9,stroke:#7DCEA0,stroke-width:2px,color:#333 style C fill:#D7E9FF,stroke:#6495ED,stroke-width:2px,color:#333 style D fill:#FFE3E3,stroke:#FF6B81,stroke-width:2px,color:#333 style E fill:#E0FFE0,stroke:#2ECC71,stroke-width:2px,color:#333 style F fill:#ECE2F9,stroke:#8A2BE2,stroke-width:2px,color:#333
İstatistiksel algoritmaların formüllerini, işlem basamaklarını, grafiklerin Python kodlarını ayrıntılı açıklamak bu yazının kapsamı dışındadır. Ayrıca, yapay zekâ ve makine öğrenmesinde kullanılan başka algoritmalar da vardır. Amaç, istatistiğin yapay zekâda nasıl kullanıldığı konusunda genel bir kavrayış oluşturmak, istatistiğin önemini vurgulamaktır.
Algoritmalar:
- Doğrusal Regresyon (Linear Regression)
- Lojistik Regresyon (Logistic Regression)
- K-Ortalama Kümeleme (K-Means Clustering)
- Karar Ağaçları (Decision Trees)
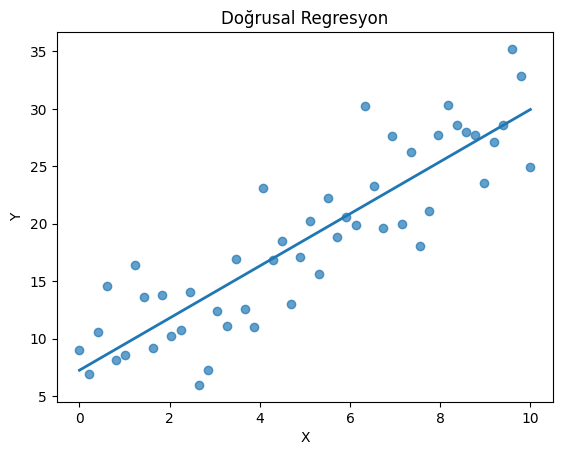
1. Doğrusal Regresyon (Linear Regression)
İstatistikte doğrusal regresyon, bir bağımlı değişken ($Y$) ile bir veya daha fazla bağımsız değişken ($X$) arasındaki doğrusal ilişkiyi modellemek için kullanılan temel bir tekniktir. Amaç, değişkenler arasındaki ilişkiyi en iyi şekilde temsil eden düz bir çizgi (regresyon doğrusu) bulmaktır, böylece bağımsız değişkenlerin değerlerine dayanarak bağımlı değişkenin değerini tahmin edebiliriz.
Bu yaklaşım; öngörü (prediction), eğilim analizi ve nedensellik ipuçları üretmek için istatistikte uzun zamandır kullanılan bir “iskelet model”dir.
Makine öğrenmesinde, daha karmaşık modeller bile çoğu zaman doğrusal bir çekirdeği optimize eder ya da karar sınırlarını yerel doğrusal parçalara ayırır. Dolayısıyla doğrusal regresyon, hem yorumlanabilirlik (parametrelerin anlamı) hem de iyi bir başlangıç performansı sağladığı için kritik önemdedir.
# Kodların çalışması için önceden yüklenmiş Python modülleri çağırılıyor.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans
from sklearn import tree
from sklearn.datasets import load_iris, make_moons
from sklearn.tree import plot_tree
from sklearn.ensemble import RandomForestClassifier
from sklearn.linear_model import LinearRegression, LogisticRegression
# Doğrusal model
np.random.seed(42)
x = np.linspace(0, 10, 50)
y = 2.5 * x + 7 + np.random.normal(scale=4, size=x.shape)
coef = np.polyfit(x, y, deg=1)
y_hat = np.polyval(coef, x)
plt.figure()
plt.scatter(x, y, alpha=0.7)
plt.plot(x, y_hat, linewidth=2)
plt.title('Doğrusal Regresyon')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()
2. Lojistik Regresyon (Logistic Regression)
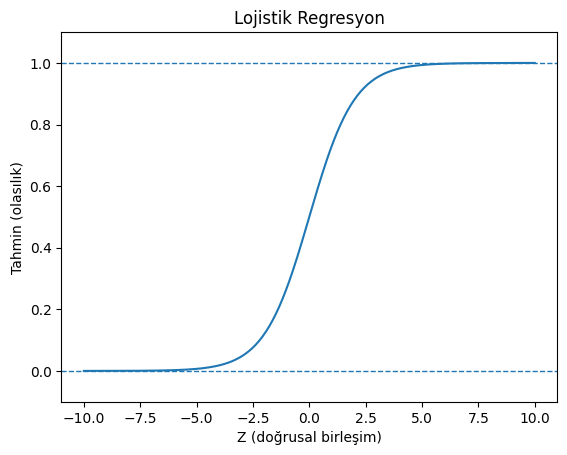
Lojistik regresyon, bağımlı değişkenin kategorik olduğu (özellikle ikili/binary, yani sadece iki olası sonucun olduğu) durumlarda kullanılan bir istatistiksel modeldir. Temel amacı, bağımsız değişkenlerin değerlerine dayanarak bir olayın gerçekleşme olasılığını tahmin etmektir.
Lojistik regresyon, doğrusal regresyonun aksine, çıktıyı doğrudan bir sayı olarak tahmin etmek yerine, sonucu 0 ile 1 arasında bir olasılık değerine dönüştürmek için sigmoid (lojistik) fonksiyonunu kullanır. Bu olasılık daha sonra genellikle 0.5 gibi bir eşik değerle karşılaştırılarak bir sınıflandırma kararına (örneğin, “Evet” veya “Hayır”, “Başarılı” veya “Başarısız”) dönüştürülür.
Bu nedenle lojistik regresyon, bir regresyon tekniği olmasına rağmen aslında bir sınıflandırma algoritması olarak işlev görür ve pazarlama, tıp veya finans gibi alanlarda risk, kayıp veya hastalık olasılığını tahmin etmek için yaygın olarak kullanılır.
Yapay zekâ ve makine öğrenmesinde lojistik regresyon, özellikle ikili sınıflandırma problemlerinde temel bir algoritma olarak kullanılır. Basitliği, yorumlanabilirliği ve yüksek hesaplama verimliliği nedeniyle genellikle daha karmaşık modellerin başlangıç noktası olarak tercih edilir. Örneğin, e-posta filtrelemede “spam” veya “spam değil” ayrımı, kredi başvurularında “onay” ya da “red” tahmini, tıbbi tanılarda “hastalık var” veya “yok” gibi karar süreçlerinde uygulanır.
Ayrıca, lojistik regresyonun altında yatan matematiksel yapı, yapay zekâ sinir ağlarındaki aktivasyon fonksiyonları ve olasılık temelli öğrenme yöntemleri için de kavramsal bir temel oluşturur.
x = np.linspace(-10, 10, 400)
sigmoid = 1 / (1 + np.exp(-x))
plt.figure()
plt.plot(x, sigmoid)
plt.axhline(0, linestyle='--', linewidth=1)
plt.axhline(1, linestyle='--', linewidth=1)
plt.title('Lojistik Regresyon')
plt.xlabel('Z (doğrusal birleşim)')
plt.ylabel('Tahmin (olasılık)')
plt.ylim(-0.1, 1.1)
plt.show()
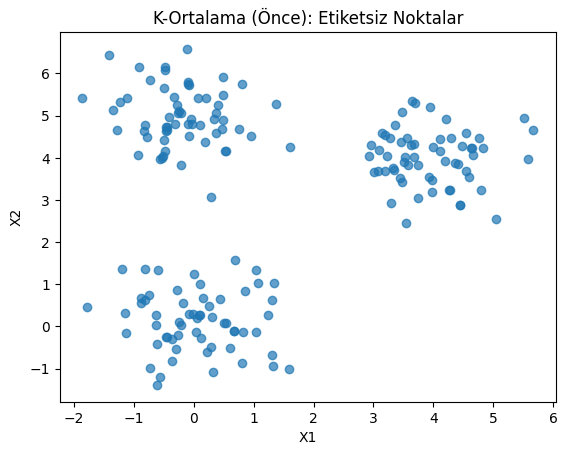
3. K-Ortalama Kümeleme (K-Means Clustering)
İstatistikte K-Ortalama Kümeleme (K-Means Clustering), verilerdeki benzer gözlemleri (veri noktalarını) önceden belirlenmiş $K$ sayıda gruba (kümelere) ayırmayı amaçlayan popüler bir kümeleme algoritmasıdır.
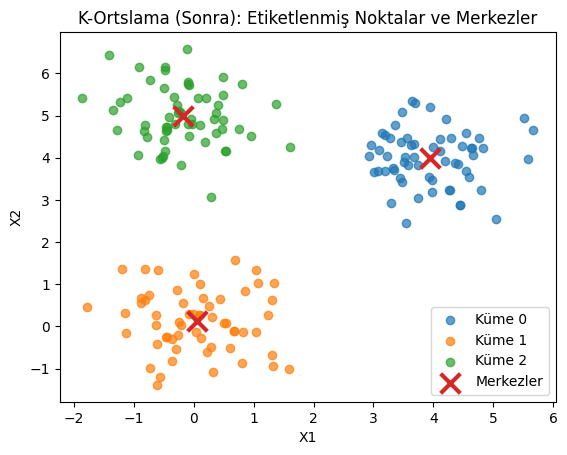
K-Ortalama, verilen $N$ adet veri noktasını, yine bir girdi parametresi olan $K$ adet kümeye böler. Algoritmanın temel amacı, her bir kümedeki veri noktalarının kendi küme merkezlerine (centroid) olan uzaklıklarının karelerinin toplamını minimuma indirmektir. Başlangıçta rastgele seçilen $K$ merkez noktasıyla başlar ve tekrar eden (iteratif) adımlarla çalışır:
- Atama Adımı: Her veri noktası, kendisine en yakın olan küme merkezine atanır.
- Güncelleme Adımı: Her küme için, kümedeki tüm noktaların ortalaması alınarak yeni küme merkezi (centroid) hesaplanır ve eski merkez buraya kaydırılır.
Bu adımlar, küme merkezleri artık önemli ölçüde değişmeyene veya maksimum iterasyon sayısına ulaşılana kadar tekrarlanır. Sonuç, küme içi benzerliğin yüksek, kümeler arası farklılığın yüksek olduğu $K$ adet ayrık kümedir.
Yapay zekâda K-Ortalama ön-analiz, veri özetleme, temsilci örnek seçimi, görselleştirme ve hatta başka algoritmalar için ön-özellik üretimi (feature engineering) gibi aşamalarda kritik rol oynar.
# Yapay veri (3 kümeye yakın)
rng = np.random.RandomState(0)
cluster1 = rng.normal(loc=[0, 0], scale=0.7, size=(60, 2))
cluster2 = rng.normal(loc=[4, 4], scale=0.7, size=(60, 2))
cluster3 = rng.normal(loc=[0, 5], scale=0.7, size=(60, 2))
X = np.vstack([cluster1, cluster2, cluster3])
# Önce: etiketsiz dağılım
plt.figure()
plt.scatter(X[:, 0], X[:, 1], alpha=0.7)
plt.title('K-Ortalama (Önce): Etiketsiz Noktalar')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
# Sonra: KMeans ile etiketleme
kmeans = KMeans(n_clusters=3, n_init=10, random_state=0)
labels = kmeans.fit_predict(X)
centers = kmeans.cluster_centers_
plt.figure()
for k in np.unique(labels):
idx = labels == k
plt.scatter(X[idx, 0], X[idx, 1], alpha=0.7, label=f'Küme {k}')
plt.scatter(centers[:, 0], centers[:, 1], marker='x', s=200, linewidths=3, label='Merkezler')
plt.legend()
plt.title('K-Ortslama (Sonra): Etiketlenmiş Noktalar ve Merkezler')
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
4. Karar Ağaçları (Decision Trees)
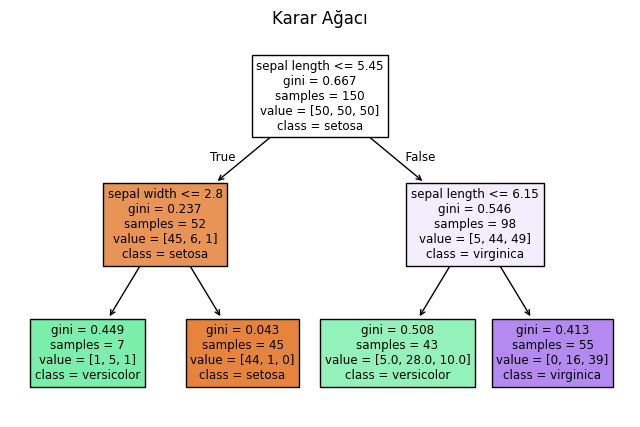
Karar ağacı, bir hedef değişkenin değerini (çıktı), girdi değişkenlerinin (özelliklerin) değerlerine dayanarak tahmin eden, akış şemasına benzeyen bir yapıdır. Adından da anlaşılacağı gibi, her bir karar düğümünün (node) potansiyel sonuçları gösteren dallara (branch) ayrıldığı bir ağaç yapısı oluşturur.
Karar Düğümü (Decision Node), veriyi belirli bir özelliğe göre iki veya daha fazla alt kümeye bölen bir test koşuludur (örneğin, “Gelir > 50.000 TL mi?”).
Dal (Branch), bu testin sonucunu temsil eden yoldur (örneğin, “Evet” veya “Hayır”).
Yaprak Düğüm (Leaf/Terminal Node), ağacın sonunu temsil eder ve veri kümesindeki bir gözlem için nihai tahmini (bir sınıf etiketi veya sayısal bir değer) içerir.
Algoritma, veriyi sürekli olarak en iyi bölme noktalarını bularak alt kümelere ayırır. “En iyi bölme”, genellikle bir kümedeki safsızlığı (homojen olmama durumunu) en aza indiren (sınıflandırma için Entropi veya Gini İndeksi kullanarak) veya varyansı en aza indiren (regresyon için) bölme olarak tanımlanır.
Karar Ağaçları, istatistikte ve makine öğreniminde hem sınıflandırma hem de regresyon problemleri için kullanılan, denetimli öğrenmeye ait önemli bir algoritma türüdür.
Karar ağaçları tek başlarına kullanılabilse de, günümüzde genellikle Rastgele Orman (Random Forest) veya Gradyan Yükseltme (Gradient Boosting) gibi daha güçlü topluluk (ensemble) algoritmalarının temelini oluşturur. Bu topluluk yöntemleri, birden çok karar ağacının tahminlerini birleştirerek tek bir ağacın dezavantajlarını (özellikle aşırı uyum/overfitting eğilimi ve kararsızlık) önemli ölçüde azaltır.
iris = load_iris()
X = iris.data[:, :2] # basitlik için ilk iki özellik
y = iris.target
# max_depth parametresini küçülterek ağacı basitleştiriyoruz.
clf = tree.DecisionTreeClassifier(max_depth=2, random_state=0)
clf.fit(X, y)
plt.figure(figsize=(8, 5))
plot_tree(clf, feature_names=['sepal length', 'sepal width'], class_names=iris.target_names, filled=True) # filled=True eklendi
plt.title('Karar Ağacı')
plt.show()
Sonuç
Bu bölümde istatistiğin yapay zekâ ve makine öğrenmesindeki temel rolünü vurgulamak amacıyla dört temel istatistiksel makine öğrenmesi algoritması tanıtıldı: Doğrusal Regresyon, Lojistik Regresyon, K-Ortalama Kümeleme ve Karar Ağaçları.
Doğrusal Regresyon, sürekli değişkenler arasındaki doğrusal ilişkileri modelleyerek tahminler yapmamızı sağlayan temel bir regresyon tekniğidir. Lojistik Regresyon, ikili sınıflandırma problemlerinde olasılık tahminleri yaparak kategorik sonuçları sınıflandırmak için sigmoid fonksiyonunu kullanan bir algoritmadır. K-Ortalama Kümeleme, denetimsiz öğrenme bağlamında veri noktalarını benzerliklerine göre gruplandıran etkili bir kümeleme yöntemidir. Karar Ağaçları ise hem sınıflandırma hem de regresyon için kullanılan, karar verme sürecini ağaç benzeri bir yapıyla modelleyen ve genellikle daha güçlü topluluk modellerinin temelini oluşturan bir algoritmadır.
Bu algoritmalar, yapay zekânın karmaşık veri setlerini anlaması, örüntüleri belirlemesi ve bilinçli kararlar alması için gerekli istatistiksel araçları sağlamaktadır. İstatistiksel temellerin anlaşılması, makine öğrenmesi modellerinin doğru bir şekilde uygulanması, yorumlanması ve geliştirilmesi için kritik öneme sahiptir.
| Algoritma | Temel İşlev, Kullanım Alanı |
|---|---|
| Doğrusal Regresyon | Sürekli değişkenler arasındaki doğrusal ilişkiyi modelleme, tahmin. |
| Lojistik Regresyon | İkili sınıflandırma, olasılık tahmini. |
| K-Ortalama Kümeleme | Veri noktalarını benzerliklerine göre kümeleme. |
| Karar Ağaçları | Hem sınıflandırma hem de regresyon, karar süreçlerini modelleme. |
İstatistiksel Öğrenme ve Makine Öğrenmesi: Detaylı Bir Karşılaştırma
İstatistiksel öğrenme (Statistical Learning) ve makine öğrenmesi (Machine Learning), veri biliminin temel taşlarıdır ve modern dünyada veriden değer yaratmanın merkezinde yer alırlar. Her ikisi de veriden desenleri ve ilişkileri keşfetme amacı taşırken, kökenleri, temel felsefeleri ve birincil odak noktaları açısından belirgin farklılıklar gösterirler. Bu yakından ilişkili alanlar, genellikle veri bilimcileri tarafından birlikte kullanılır, ancak hangi aracın hangi amaca daha uygun olduğunu anlamak kritik öneme sahiptir.
1. İstatistiksel Öğrenme (Statistical Learning): Nedenleri Anlamak
Odak Noktası: İstatistiksel öğrenme, adından da anlaşılacağı gibi, istatistiksel teori ve yöntemlerden beslenir. Temel amacı, bir veri setinin altında yatan gerçek veri üretim sürecini (data generating process) anlamak ve açıklamaktır. Yani, olayların neden bu şekilde gerçekleştiğini, değişkenler arasındaki ilişkinin doğasını ve bu ilişkilerin istatistiksel olarak ne kadar önemli olduğunu ortaya çıkarmak ister.
- Çıkarım ve Yorumlama: İstatistiksel öğrenmenin kalbinde çıkarım (inference) ve yorumlama (interpretation) yer alır. Bir model oluşturulduğunda, bu modeldeki her bir parametrenin (örneğin, regresyon katsayıları) anlamı, yönü ve büyüklüğü titizlikle incelenir. Hangi değişkenlerin hedef değişken üzerindeki etkisinin istatistiksel olarak anlamlı olduğu, bu etkinin yönü (pozitif mi, negatif mi) ve büyüklüğü (ne kadar güçlü) belirlenir. Güven aralıkları ve p-değerleri gibi istatistiksel ölçümler, bu çıkarımların güvenilirliğini değerlendirmek için kullanılır.
- Teorik Temeller: Kökeni, 17. yüzyıldan bu yana gelişen matematiksel istatistik ve olasılık teorisine dayanır. Regresyon analizi, varyans analizi (ANOVA), hipotez testleri gibi klasik istatistiksel yöntemler bu alanın temelini oluşturur.
- Model Şeffaflığı: Genellikle daha yorumlanabilir (interpretable) modeller tercih edilir. Modelin nasıl çalıştığı, çıktıların hangi inputlardan geldiği ve bu inputların çıktı üzerindeki etkisi net bir şekilde anlaşılmalıdır. Bu, “kara kutu” (black box) modellerinden kaçınıldığı anlamına gelir.
- Uygulama Alanları: Sosyal bilimler, ekonomi, tıp araştırmaları, pazar araştırmaları ve kamu politikası oluşturma gibi alanlarda yaygın olarak kullanılır. Örneğin, bir ilacın etkinliğini anlamak, eğitim seviyesinin gelir üzerindeki etkisini açıklamak veya bir pazarlama kampanyasının satışları nasıl etkilediğini belirlemek istendiğinde istatistiksel öğrenme yaklaşımları tercih edilir.
2. Makine Öğrenmesi (Machine Learning): En İyi Sonuçları Elde Etmek
Odak Noktası: Makine öğrenmesi ise, bilgisayar bilimleri ve yapay zeka alanının bir alt dalı olarak gelişmiştir. Birincil amacı, veriden otomatik olarak öğrenen ve belirli bir görevi (tahmin, sınıflandırma, kümeleme vb.) en yüksek performansla yerine getiren algoritmalar geliştirmektir. Burada “neden” sorusu yerine, “en iyi sonuçları nasıl elde edebilirim?” sorusu ön plandadır.
- Tahmin ve Karar Verme: Makine öğrenmesinin ana hedefi, yeni, daha önce görülmemiş veriler üzerinde doğru tahminler yapmak veya en iyi kararları vermektir. Tahminin veya kararın arkasındaki nedeni tam olarak açıklamak genelde ikincil bir öneme sahiptir, birincil olan doğruluğudur.
- Performans ve Ölçeklenebilirlik: Algoritmalar, büyük ve karmaşık veri setlerinde (Big Data) bile hızlı ve verimli çalışacak şekilde tasarlanır. Modelin hata oranı (accuracy, precision, recall, F1-score gibi metrikler) minimize edilmeye çalışılır ve algoritmaların daha fazla veriyle veya daha karmaşık problemlerle başa çıkabilme yeteneği (ölçeklenebilirlik) kritiktir.
- Algoritmik Temeller: Kökeni, bilgisayar bilimleri, yapay zeka ve matematiksel optimizasyon teorisine dayanır. Karar ağaçları, destek vektör makineleri (SVM), sinir ağları (neural networks), rastgele ormanlar (random forests) ve gradyan yükseltme (gradient boosting) gibi algoritmalar bu alanın tipik örnekleridir.
- Kara Kutu Modelleri: Performans odaklı yaklaşım, bazen modelin iç işleyişinin karmaşık ve yorumlanmasının zor olduğu “kara kutu” modellerine yol açabilir. Bu modeller, neden belirli bir tahmin yaptıklarını açıklamakta zorlanabilir, ancak genellikle son derece doğru tahminler sunarlar.
- Uygulama Alanları: Spam tespiti, yüz tanıma, doğal dil işleme, tavsiye sistemleri (Netflix, Amazon), otonom araçlar, dolandırıcılık tespiti ve tıbbi görüntü analizi gibi geniş bir yelpazede kullanılır. Örneğin, bir e-postanın spam olup olmadığını doğru bir şekilde sınıflandırmak, bir görüntünün içindeki nesneyi tanımak veya bir müşteriye hangi ürünün önerileceği gibi konularda makine öğrenmesi algoritmaları devreye girer.
Ortak Zemin ve Sinerji: İki Alan Nasıl Buluşur?
Modern veri bilimi uygulamalarında istatistiksel öğrenme ve makine öğrenmesi arasındaki sınırlar giderek bulanıklaşmaktadır. Aslında, “istatistiksel öğrenme” terimi, hem istatistiksel modelleme hem de algoritmik yaklaşımları bir araya getiren bir şemsiye terim olarak da kullanılmaktadır.
- Ortak Yöntemler: Hem istatistiksel öğrenme hem de makine öğrenmesi birçok ortak algoritma ve tekniği kullanır. Örneğin, Doğrusal Regresyon (Linear Regression), Lojistik Regresyon (Logistic Regression), K en Yakın Komşu (K-NN) ve hatta bazı Karar Ağacı algoritmaları her iki alanda da incelenir ve uygulanır.
- Birbirini Tamamlama:
- İstatistiksel öğrenme, bir makine öğrenmesi modelinin performansını etkileyen temel ilişkileri anlama konusunda valuable insights sağlayabilir. Yani bir ML modelinin neden iyi veya kötü çalıştığını anlamak için SL araçları kullanılabilir.
- Makine öğrenmesi, istatistiksel modellerin tahmin yeteneklerini artırmak veya çok büyük, karmaşık veri setleriyle başa çıkmak için kullanılabilir.
- “İstatistiksel Öğrenme” Disiplini: Bazı akademisyenler “istatistiksel öğrenme”yi, makine öğrenmesi algoritmalarına istatistiksel kesinliği ve yorumlanabilirliği getiren bir alan olarak tanımlar. Bu, özellikle bilgisayar bilimleri kökenli makine öğrenmesi yaklaşımlarına, istatistiksel modelleme ve çıkarım araçlarını uygulayarak onların “neden” sorusuna da cevap verebilmesini sağlamaya çalışır.
Sonuç
Özetle, istatistiksel öğrenme “neden” sorusuna odaklanarak verinin altında yatan yapıyı ve değişkenler arasındaki ilişkileri anlamaya çalışırken; makine öğrenmesi “nasıl” sorusuna odaklanarak en iyi tahminleri veya kararları verecek algoritmaları geliştirmeye çalışır. Her ikisi de veri biliminin vazgeçilmezidir ve genelde pratik sorunları çözmek için birlikte kullanılırlar. İyi bir veri bilimcisi, elindeki soruna, veriye ve ulaşmak istediği amaca göre bu iki perspektif arasında doğru dengeyi kurabilen kişidir.
Birçok makine öğrenmesi algoritması istatistiksel öğrenmeden türemiştir veya istatistiksel ilkelere dayanır. İlk bölümde ele aldığımız Doğrusal Regresyon, Lojistik Regresyon, K-Ortalama Kümeleme ve Karar Ağaçları gibi algoritmalar bu kesişimin en güzel örneklerindendir. Bu algoritmalar hem verideki ilişkileri anlamamıza (istatistiksel öğrenme) hem de bu ilişkileri kullanarak gelecekteki olayları tahmin etmemize veya verileri organize etmemize (makine öğrenmesi) olanak tanır. Dolayısıyla, güçlü ve güvenilir bir makine öğrenmesi uygulaması geliştirmek için istatistiksel temelleri ve her iki yaklaşımın güçlü yönlerini anlamak vazgeçilmezdir.